Project 2: Fun with Filters and Frequencies

Overview

Our project scope explores different utilies of frequencies. It walks us through the process of filtering to find an image's edges, sharpening a blurry image, creating hybrid pictures, and ultimately using blending techniques to mix images together

Part 1.1: Finite Difference Operator

We begin with the most basic ways to filter through an image. It is effectively utilizing the arrays [1, -1]T and [1, -1] that leaves what can be described as "complimentary remnants" after being convolved with the original image. Afterwards, we combined the gradient by using a simple magnitude formula to combine the two derivatives

We have also tried binarizing the image according to many different thresholds to see which would be the best. In the end, my own judgement thought 45 was the best

Threshold Attempts — From left to right: Thresholds at 10, 30, 50, 70, and 100

Final Threshold Image — Final Threshold at 45

Counterintuitively, it was found that it was more helpful to find a more accurate outline of the image when we blurred the image first. This allowed for more data to be gathered to create more complex lines

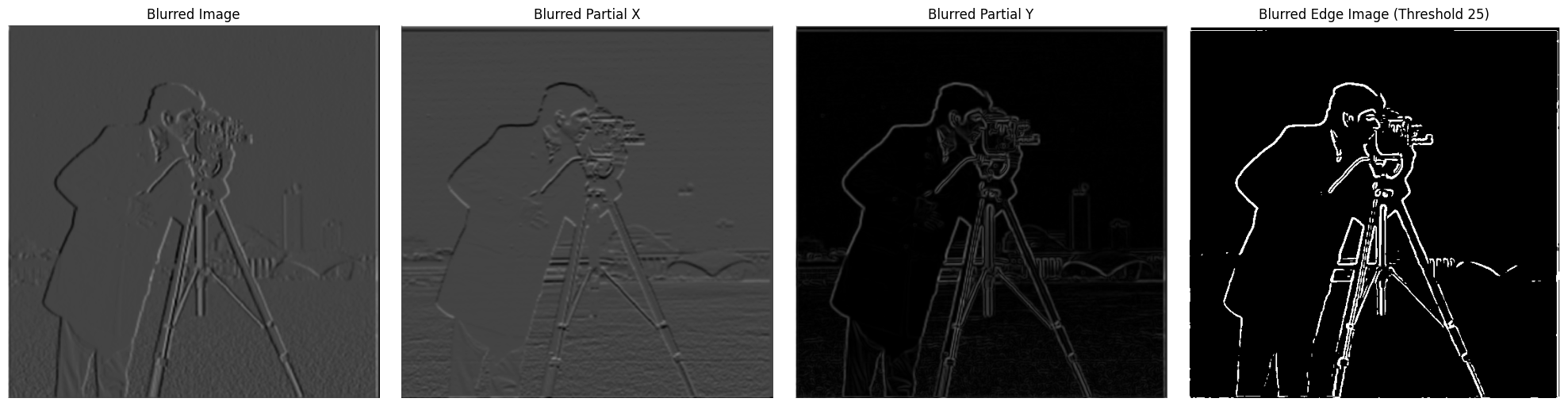
Lastly, rather than the basic filter, we now use a gaussian partial, which ended up being the best image

DoG Filters — From left to right: DoG Filter in X, DoG Filter in Y, DoG Gradient Magnitude, DoG Edge Image (Threshold 25)

Part 2: Fun with Frequencies

To sharpen an image, we are looking to try and bring out the high frequency instances of the image. In effect. we blur the image using Gaussian Blur and afterwards subtract these values from the original image through the use of the addWeighted function. To see the effectiveness, I also opted to try a list of several different alpha values to show the differences/development of "sharpness"

Sharpening Taj and Chopper with Different Alphas

Taj and Chopper Sharpened with Alpha = 1.0, 3.0, 6.0

Not only did we sharpen an image that wasn't clear, but also tested blurring an image ourselves then resharpened it. Ideally, our before and after should be the same, but as we see in effect, blurring the image adds a bit of unexpected noise. So resharpening it left us with lower quality than the original.

Blurring and Re-sharpening Monster

Blurred and Resharpened Monster — Monster: Blurred and Resharpened

Part 2.2: Hybrid Images

Here we are creating hybrid images. The process of which is to obtain the low and high frequency images, then try to overlay them atop of one another. The process of obtaining low and high frequency images is similar to what we have done in similar parts, and we aligned them using provided functions by the staff

Nutmeg and Derek

When creating hybrid images, I've tried a combination of which frequency has color or not. After a bit of testing, visually speaking I prefer the one with both having color the most. Though this is completely subjective.

Low Frequency Image — Low Frequency Hybrid

High Frequency Derek — High Frequency Hybrid

XPP and Popplio (Failure)

This attempt simply did not look as smooth as I would have desired. I think the Popplio's blocky shape and more pronounced colors contrasted the xpp a bit too much. I tried a different combination of having it be both the low and high frequency image, but neither seem to have worked that well. Even when shifting colors around. I put when neither had color becausem I thought it was an especially funny failure, but it simply didn't work well.

Gojo and Jogo

This one was my favorite. It really helped that the meme already put it in a similar format, so it seemed like not matter what combination I picked the image always turned out well. It was just a matter of lowering Gojo's frequency a lot because it was pretty sharp inherently compared to jogo. So many values jsut led to only gojo appearing.

As such, we also showed the Fourier transformations of the low and high frequencies as well as their filtered versions

FT High Frequency — Fourier Transform High Frequency

FT Low Frequency — Fourier Transform Low Frequency

FT Hybrid — Fourier Transform Hybrid Image

Part 2.3: Gaussian and Laplacian Stacks

This section showcases the Gaussian and Laplacian stacks used for multiresolution blending. Below are the representations of these stacks at various levels for a given image.

Part 2.4: Multiresolution Blending (a.k.a. the Oraple)

The blending of images in this example leverages Gaussian and Laplacian stacks to create multiresolution images. First, Gaussian stacks are constructed for each input image, which progressively blur the image across multiple levels, maintaining the original image resolution. Using these Gaussian stacks, Laplacian stacks are then generated by subtracting each level of the Gaussian stack from the next finer level, which captures the detail lost between blurring steps, and finally, these multi-level details from one image are combined with the smoothed versions from another image to achieve a seamlessly blended result. This method allows for the integration of different spatial frequencies from each source image, ensuring a smooth transition across the combined image.